Блокчейн: атаки, безопасность и криптография

В одной из прошлых статей мы уже касались тем технологии блокчейна, биткоина и сопутствующего им окружения. И спустя это время блокчейн не только не растерял своей привлекательности, но и вовсе стал одним из новых трендов в финансовом секторе и ИТ-индустрии. Крупнейшие российские банки Альфа банк и Сбербанк известили о проведении первой транзакции основанной на блокчейне. Международные платежные системы VISA, Mastercard, Unionpay и SWIFT сообщили о совместных разработках в этой области. А в июле 2017 года лидеры в своих отраслях, компании S7 Airlines и Альфа Банк и вовсе запустили в эксплуатацию блокчейн-платформу по автоматизации торговых операций с агентами на базе приватной сети Ethereum.

Однако, с ростом популярности блокчейна (и в частности криптовалюты Биткоина, основанной на блокчейне) многократно возросли и хакерские атаки, различные попытки мошенничества и кражи виртуальной наличности. Все это безусловно заставляет задуматься экспертов и разработичков о безопасности блокчейна как перспективной технологии.

Сегодня в статье мы предлагаем чуть более подробно рассмотреть потенциальные атаки на блокчейн как технологию, а так же продукты и сервисы основанные на нем. И конечно же чуть глубже заглянем внутрь его криптографической сердцевины, как основы обеспечения безопасности крипто вычислений

Пару слов о технологии

Прежде чем перейти непосредственно к вопросам безопасности буквально пару кратеньких абзацев о самой технологии Блокчейн простым языком.

Как говорят нам авторитетные источники, технология BlockChain (блокчейн) появилась по ИТ-шным меркам достаточно давно, а именно в 2009 году. И спустя некоторое время  громогласно на весь мир заявила о своем существовании, к примеру наиболее ярко проявив себя в качестве технологической платформы для криптовалюты, коим сейчас является биткоин. 

Если не вдаваться в сложные формулировки и математическое описание, то Блокчейн (blockchain) – это по сути распределенная база данных, состоящая из множества блоков информации сгенерированным таким образом, что несанкционированная их модификация или удаление практически невозможно.

Фича этой технологии в том, что после того как блоки данных были опубликованы в реестре, используя криптографические функции, штампы времени и ссылки на предыдущий блок (связанная цепочка блоков) откатить их назад или же внести какие-то изменения в запись невозможно. Достигается это за счет того, что все вычисления децентрализованны, то есть нет единого управляющего центра и монопольной власти над вычислениями. К тому же вся информация о вычислениях хранится в сети сразу же у нескольких участников (так называемых майнеров). Хотя само содержимое блоков не зашифровано и доступно в открытом виде, данные в блоке защищены криптографически через хэш-цепочки. А децентрализованная база публично хранит в незашифрованном виде полную информацию о всех современных транзакциях, подписываемых с помощью асимметричного шифрования.

Поэтому ключевыми преимуществами блокчейна часто называют  прозрачность процесса транзакций и множественное дублирование информации о транзакциях у каждого участника процесса. Отсюда и вывод почему нельзя выполнить подделку транзакции или ее удаление из базы данных (реестра).

Блокчейн уже сегодня стал технологической платформой для платежных систем, умных контрактов,  а в перспективе называются такие отрасли как управление данными, средства электронного голосования, проверка подлинности и подтверждение прав доступа, прогнозирование, онлайн-сервисы (соц сети, музыка, и т.д.), торговля ценными бумагами и даже совместное использование автомобилей.

В ИТ-индустрии  блокчейн нашел себя прежде всего в сфере хранения и подтверждение данных, к примеру, то, что в настоящее время используется для интеллектуального анализа данных (дата-майнинг). 

Некоторые технические основы блокчейна

Опять же не в даваясь в сложные технические подробности в начале небольшой ликбез по основным техническим моментам технологии Блокчейн. Это позже поможет понять нам в чем же могут быть проблемы безопасности.  И так, поехали!

Как мы уже выше выяснили Блокчейн использует для вычислений  и защиты блоков криптографические функции. Рассмотрим чуть ближе понятия "цифровая подпись" и "хеш-цепочка".

Если взять определение из ФЗ-63 "О цифровой подписи", то

Электронная подпись (ЭП) – это особый реквизит документа, который позволяет установить отсутствие искажения информации в электронном документе с момента формирования ЭП и подтвердить принадлежность ЭП владельцу. Значение реквизита получается в результате криптографического преобразования информации.

Как работает цифровая подпись?

И так, каждый человек для общения в Интернете или обмена данными с другими пользователями посредством компьютера и теллекомуникационных каналов связи может создать себе «личный идентификатор» (ID, никнейм) и «цифровую подпись», подтверждающее подлинность автора. 

Электронная подпись позволяет:

• Подтвердить авторство отправителя сообщения 

• Гарантировать, что отправленное и подтвержденное через ЭП сообщение никто не сможет подделать

Итак, закрытым ключом мы подписываем «письма передачи прав собственности» (транзакции), и тем самым, к примеру отдаем свои монеты кому-то другому. Открытым ключом  (сертификат) мы проверяем подлинность чужих транзакций.

Хэширование (англ. hashing) — преобразование массива входных данных произвольной длины в (выходную) битовую строку фиксированной длины. Функция, реализующая алгоритм и выполняющая преобразование, называется «хеш-функцией» или «функцией свёртки». Исходные данные называются входным массивом, «ключом» или «сообщением». Результат преобразования (выходные данные) называется «хешем», «хеш-кодом», «хеш-суммой», «сводкой сообщения». 

Криптографическая хеш-функция — всякая хеш-функция, являющаяся криптостойкой, то есть удовлетворяющая ряду требований, специфичных для криптографических приложений.

Как работает хеширование?

Показать хеширование довольно просто. Возьмем некоторое число… например номер телефона +7 (495) 606-36-02. Сложим все цифры вместе, несколько раз:

7+4+9+5+6+0+6+3+6+0+2=48 => 4+8=12 => 1+2=3

Так можно однозначно сопоставить любому номеру телефона некоторое число. Процесс суммирования называется хешированием, сам способ — хеш функцией, полученное число — хеш-суммой или просто хешем.

Обычно добиваются следующий свойств от хеширования:

• Зная хеш-сумму (в нашем случае 3) нельзя определить исходный номер телефона.
• Нельзя подогнать номер телефона под заранее известную сумму (в нашем примере неприменимо, обязательно для bitcoin).
• Малое изменение номера телефона приведет к кардинальному изменению хеша (в нашем примере неприменимо, но обязательно для bitcoin).

Данный пример взят из статьи на Хабре.

Сложность вычислений

За требование к хешам блоков отвечает специальный параметр, называемый «сложность». Так как вычислительные мощности сети непостоянны, этот параметр пересчитывается клиентами сети через каждые 2016 блоков таким образом, чтобы поддерживать среднюю скорость формирования блокчейна на уровне 2016 блоков в две недели.

Таким образом, 1 блок должен создаваться примерно раз в десять минут. На практике, когда вычислительная мощность сети растёт — соответствующие временные промежутки короче, а когда снижается — длиннее. Перерасчёт сложности с привязкой ко времени возможен благодаря наличию в заголовках блоков времени их создания. 

Атаки на Блокчейн и проблемы безопасности

Любые новые технологии всегда несут не только блага для цивилизации, но и содержат в себе новые риск,  в том числе риски связанные с информационной безопасностью. 

Блокчейн, по мимо ИТ-феномена еще и явление социальное, вспомните хотя бы хайп вокруг биткоина и майнинг-фермы в Китае! А как известно в любой социальной группе рано или поздно происходят  попытки обмана (мошенничества).

И так рассмотрим наиболее реалистичные и ключевые атаки на технологию Блокчейн и продукты построенные на его основе.

Атака 51% 

Суть атаки в том, что злоумышленник, контролируя более пятидесяти процентов подтверждающих ресурсов блокчейн-сети, может напечатать свою цепочку блоков, которая обгонит основную цепочку блокчейна и в результате станет основной. При этом он легко и беспрепятственно отменит часть транзакций, сделанных в отброшенных им блоках. Например, транзакции о денежных переводах. Таким образом, теоретически можно отменить транзакцию задним числом.

По сути майнинг подобен перебору лотерейных билетов. С разной вероятностью выигрыша. Так что для успешной атаки можно иметь даже меньше 51 процента мощности. Вероятность успеха при этом будет падать, но преступник может надеяться, что ему повезет.

На ранних этапах своего развития Биткоин и любая подобная ей валюта уязвима к так называемой «Атаке 51%»: пока в распоряжении атакующего находятся мощности большие, чем у всей остальной сети, то он сможет не подтверждать чужие блоки, подтверждая только свои, а значит получать 100 % всех новых биткоинов и блокировать по своему усмотрению любые транзакции. На данный момент для осуществления такой атаки в сети Bitcoin требуется вычислительная мощность во много раз превышающая мощность всех суперкомпьютеров из рейтинга TOP-500.

Атаки на отказ  в обслуживании (DoS)

Отправка большого количества "мусорных" данных на узел, обрабатывающий транзакции, может усложнить его работу. Например, клиент Bitcoin Satoshi версии 0.7.0 блокирует все подозрительные узлы и транзакции, не позволяет дублировать транзакции, контролирует появление атаки DoS, ловит в системе злоумышленников, исправляет ошибки и т.д. 

Взлом крипто алгоритмов хэш-функций

Алгоритмы для вычисления хэш-функции стандартов SHA-256 и ECDSA считаются весьма стойкими при существующих вычислительных мощностях. Однако, появление высокопроизводительных квантовых компьютеров увеличит риск взлома этих криптографических функций. 

Атака Сибиллы

Хакер может попытаться наполнить сеть подконтрольными ему узлами, и остальные пользователи смогут подключиться только к блокам, созданным для мошенничества. К примеру, Атакующий блокирует транзакции от других пользователей, отсоединив вас от общей сети. После этого Атакующий подсоединяет вас только к блокам, которые создает он, в отдельной сети. В результате этого будут появляться транзакции, которые будут пересылать деньги повторно (double-spending).

Замедление времени в системе

Сценарий этой атаки такой, хакеры атакуют сеть в которой находятся абоненты блокчейн продукта, к примеру, биткоина,  и путем создания большой вычислительной нагрузки на систему замедляют время внутри сети, что усложняет передачу данных, сообщений между пользователями, обновление информации в сети, формирование блоков, цепочек и их фиксацию участниками транзакций.

Уязвимость транзакций

Несмотря на то, что транзакции в Bitcoin подписываются, эта подпись охватывает не всю информацию, которая хешируется для получения хеша транзакции. Фактически, существуют возможность изменить параметры транзакции так, что изменится хеш, но подпись останется прежней.

На основе этого может быть организована атака при выводе средств со сторонних сервисов. В исходной транзакции заменяется идентификатор, деньги доходят до адресата, но тот сообщает в техническую поддержку сервиса, что исходная транзакция не дошла. В результате, сервис может совершить повторную отправку средств.

Есть еще одна разновидность этой атаки получившие название  «гибкость транзакций». Суть атаки в том, что  злоумышленник изменяет уникальный идентификатор транзакции биткоинов до ее подтверждения в сети Bitcoin. При таком изменении и при соблюдении должных условий пользователь может сделать вид, что транзакция не была осуществлена.

Ошибки кода

Баги могут привести к нестабильности в защите системы. Например, в узле информация должна обновляться за короткий отрезок времени. Если из-за бага это не произошло, в цепочке не появилась нужная информация, неправильные данные начали распространяться по сети и т.д. Все это может стать причиной остановки работы сети на несколько часов.

Криптография на страже безопасности блокчейна

В настоящем абзаце сипользовалтись материалы представленые в статьях тут и вот тут, а так же тут и еще тут.

Базовая идея 

Фундаментальной частью биткойна являются конечно же криптографические алгоритмы. В частности, такой алгоритм как  ECDSA — Elliptic Curve Digital Signature Algorithm, который использует эллиптические кривые (elliptic curve) и конечные поля (finite field) для подписи данных, чтобы третья сторона могла подтвердить аутентичность подписи, исключив возможность её подделки. 

Что такое ECDSA

ECDSA — это акроним для "Алгоритма Цифровой Подписи с Эллиптическими Кривыми". Это процесс, который использует эллиптические кривые и конечные поля, чтобы «подписать» данные таким образом, что третьи лица могут легко проверить подлинность подписи, но при этом сам подписывающий оставляет за собой эксклюзивную возможность создавать подписи. В случае Биткойна «данные», которые подписываются — это транзакция, которая передает право собственности на биткойны.

ECDSA имеет две отдельные процедуры для подписи и ее проверки (т.е. верификации). Каждая процедура представляет собой алгоритм, состоящий из нескольких арифметических операций. Алгоритм подписи использует секретный ключ, а алгоритм проверки использует только открытый ключ. 

Эллиптические кривые - теория

В эллиптических кривых нет ничего сложного. Алгебраически каждая такая кривая может быть представлена как уравнение вида:

y² = x³ + ах + b

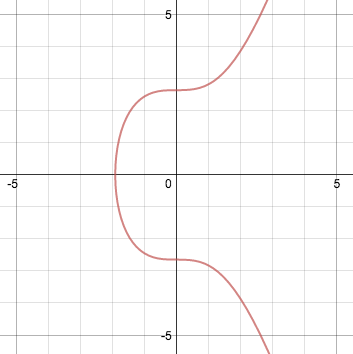
Для а = 0 и b = 7 (а это именно та версия, которую использует Биткойн) эта кривая выглядит так:

Эллиптические кривые имеют некоторые полезные свойства. Например, не-вертикальная прямая, пересекающая кривую в двух точках, всегда будет пересекать ее и в третьей точке, лежащей на кривой. Другим свойством является то, что если не-вертикальная прямая является касательной к кривой в одной из точек, то она обязательно пересекает кривую еще ровно в одной точке.

Мы можем использовать эти свойства, чтобы определить две операции над точками, составляющими кривую: сложение точек и удвоение.

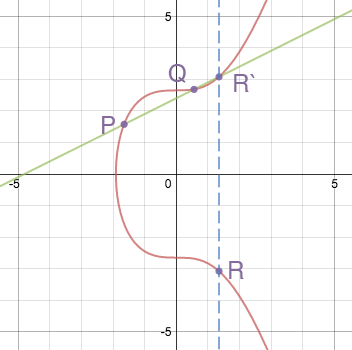
Для сложения точек, P + Q = R мы проводим через точки P и Q прямую, которая, по свойствам эллиптических кривых, пересекает кривую в некоторой третьей точке R‘. Затем мы находим точку на кривой, симметричную точке R‘ относительно оси X. Именно эта точка R и будет считаться суммой P и Q. Это легче всего понять, глядя на следующую схему:

Это все хорошо, но как бы нам сложить точку саму с собой? Для этого определяется операция удвоения точки, P + P = R. При удвоении мы проводим прямую, касательную к данной эллиптической кривой в точке P, которая, согласно свойствам кривой, должна пересекать ее еще в одной точке R‘. Точка R, симметричная R‘ относительно оси X, и будет считаться точкой удвоения P. На графике это выглядит следующим образом:

Эти две операции можно использовать, чтобы определить операцию скалярного умножения, R = a P, определяемую как добавление точки Р самой к себе a раз. Например:

R = 7P

R = P + (P + (P + (P + (P + (P + P)))))

Процесс скалярного умножения, как правило, можно упростить, используя комбинацию сложения и удвоения точек. Например:

R = 7P

R = P + 6P

R = P + 2 (3P)

R = P + 2 (Р + 2P)

Здесь операция 7P была разбита на два этапа удвоения точек и два сложения точек — в итоге, вместо 7 операций нужно произвести всего четыре.

Собственно, теперь вы знаете об эллиптических кривых все, что о них стоит знать.

Закрытый ключ - теория

Приватный ключ — это довольно общий термин и в различных алгоритмах электронной подписи могут использоваться различные типы приватных ключей.

Как вы уже могли заметить, в Bitcoin используется алгоритм ECDSA — в его случае приватный ключ — это некоторое натуральное 256 битное число, то есть самое обычное целое число от  до . Технически, даже число 123456 будет являться корректным приватным ключом, но очень скоро вы узнаете, что ваши монеты «принадлежат» вам ровно до того момента, как у злоумышленника окажется ваш приватный ключ, а значения типа 123456 очень легко перебираются.

Важно отметить, на сегодняшний день перебрать все ключи невозможно в силу того, что  — это фантастически большое число.

Постараемся его представить: согласно этой статье, на всей Земле немногим меньше  песчинок. Воспользуемся тем, что , то есть  песчинок. А всего адресов у нас , примерно .

Значит, мы можем взять весь песок на Земле, превратить каждую песчинку в новую Землю, в получившейся куче планет каждую песчинку на каждой планете снова превратить в новую Землю, и суммарное число песчинок все равно будет на порядки меньше числа возможных приватных ключей.

По этой же причине большинство Bitcoin клиентов при создании приватного ключа просто берут 256 случайных бит — вероятность коллизии крайне мала.

Открытый (публичный) ключ - теория

Пусть  — наш приватный ключ,  — base point, тогда публичный ключ . То есть, фактически, публичный ключ — это некоторая точка, лежащая на кривой SECP256k1.

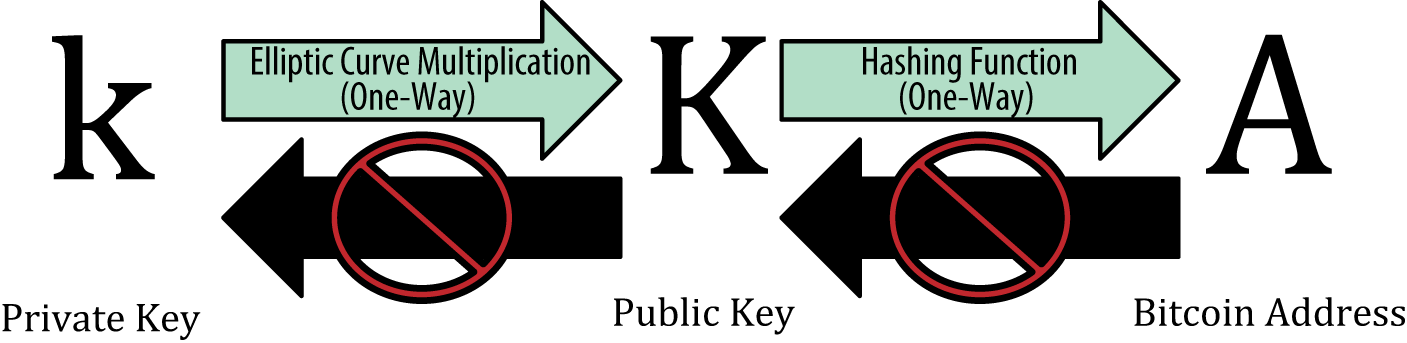
Два важных нюанса. Во-первых, несложно видеть, что операция получения публичного ключа определена однозначно, то есть конкретному приватному ключу всегда соответствует один единственный публичный ключ. Во-вторых, обратная операция является вычислительно трудной и, в общем случае, получить приватный ключ из публичного можно только полным перебором первого.

Ниже вы узнаете, что точно такая же связь существует между публичным ключом и адресом, только там все дело в необратимости хэш-функций.

ECDSA в биткойне

В протоколе биткойна зафиксирован набор параметров для эллиптической кривой и её конечного поля, чтобы каждый пользователь использовал строго определенный набор уравнений. Среди зафиксированных параметров выделяют уравнение кривой (equation), значение модуля поля (prime modulo), базовую точку на кривой (base point) и порядок базовой точки (order). О вычислении порядка базовой точки вы можете почитать здесь. Этот параметр подбирается специально и является очень большим простым числом.

В случае биткойна используются следующие значения:

Уравнение эллиптической кривой: 

y² = x³ + 7

Простой модуль: 

2256— 232 — 29 — 28 — 27 — 26 — 24 — 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F

Базовая точка:

04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8

Жирным шрифтом выделена координата X в шестнадцатеричной записи. За ней сразу следует координата Y.

Порядок: FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141

Этот набор параметров для эллиптической кривой известен как secp256k1 и является частью семейства стандартов SEC (Standards for Efficient Cryptography), предлагаемых для использования в криптографии. В биткойне кривая secp256k1 используется совместно с алгоритмом цифровой подписи ECDSA (elliptic curve digital signature algorithm). В ECDSA секретный ключ — это случайное число между единицей и значением порядка. Открытый ключ формируется на основании секретного: последний умножается на значение базовой точки. Уравнение имеет следующий вид:

Открытый ключ = секретный ключ * G

Это показывает, что максимальное количество секретных ключей (следовательно, биткойн-адресов) — конечно, и равняется порядку. Однако порядок является невероятно большим числом, так что случайно или намеренно подобрать секретный ключ другого пользователя нереально.

Вычисление открытого ключа выполняется с помощью тех же операций удвоения и сложения точек. Это тривиальная задача, которую обычный персональный компьютер или смартфон решает за миллисекунды. А вот обратная задача (получение секретного ключа по публичному) — является проблемой дискретного логарифмирования, которая считается вычислительно сложной (хотя строгого доказательства этому факту нет). 

Когда пара секретный/публичный ключ получена, её можно использовать для подписи данных. Эти данные могут быть любой длины. Обычно первым шагом выполняется хеширование данных с целью получения уникального значения с числом битов, равным битности порядка кривой (256). После хеширования, алгоритм подписи данных z выглядит следующим образом. Здесь, G — базовая точка, n — порядок, а d — секретный ключ.

• Выбирается некоторое целое k в пределах от 1 до n-1
• Рассчитывается точка (х, у) = k * G с использованием скалярного умножения
• Находится r = х mod n. Если r = 0, то возврат к шагу 1
• Находится s = (z + r * d) / k mod n. Если s = 0, то возврат к шагу 1
• Полученная пара (r, s) является нашей подписью

После получения данных и подписи к ним, третья сторона, зная публичный ключ, может их верифицировать. Шаги для проверки подписи такие (Q — открытый ключ):

• Проверка, что и r, и s находятся в диапазоне от 1 до n-1
• Рассчитывается w = s-1 mod n
• Рассчитывается u = z * w mod n
• Рассчитывается v = r * w mod n
• Рассчитывается точка (x, y) = uG + vQ
• Если r = x mod n, то подпись верна, иначе — недействительна

В самом деле,

uG + vQ = u + vdG = (u + vd)G = (zs-1 + rds-1)G = (z + rd) s-1G = kG

Последнее равенство использует определение s на этапе создания подписи.

Безопасность ECDSA связана со сложностью задачи поиска секретного ключа, описанной выше. Помимо этого, безопасность исходной схемы зависит от «случайности» выбора k при создании подписи. Если одно и то же значение k использовать более одного раза, то из подписей можно извлечь секретный ключ, что и произошло с PlayStation 3. Поэтому современные реализации ECDSA, в том числе используемые в большинстве биткойн-кошельков, генерируют k детерминировано на основе секретного ключа и подписываемого сообщения.

Отечественный  ГОСТ Р 34.10-2012 vs ECDSA

ГОСТ Р 34.10-2012  - российский стандарт, описывающий алгоритмы формирования и проверки электронной цифровой подписи. Принят и введён в действие Приказом Федерального агентства по техническому регулированию и метрологии от 7 августа 2012 года № 215-ст вместо утратившего силу предыдущего ГОСТ Р 34.10-2001. 

ГОСТ Р 34.10-2012  основан на эллиптических кривых. Стойкость этих алгоритмов основывается на сложности вычисления дискретного логарифма в группе точек эллиптической кривой, а также на стойкости хэш-функции. 

После подписывания сообщения М к нему дописывается цифровая подпись размером 512 или 1024 бит и текстовое поле. В текстовом поле могут содержаться, например, дата и время отправки или различные данные об отправителе.

Криптостойкость цифровой подписи опирается на две компоненты — на стойкость хэш-функции и на стойкость самого алгоритма шифрования.

Вероятность взлома хэш-функции по ГОСТ 34.11-94 составляет ${\displaystyle 1{,}73\times {10}^{-77}}$ при подборе коллизии на фиксированное сообщение и ${\displaystyle 2{,}94\times {10}^{-39}}$ при подборе любой коллизии. Стойкость алгоритма шифрования основывается на проблеме дискретного логарифмирования в группе точек эллиптической кривой. На данный момент нет метода решения данной проблемы хотя бы с субэкспоненциальной сложностью.

Один из самых быстрых алгоритмов, на данный момент, при правильном выборе параметров — ${\displaystyle \rho }$-метод и ${\displaystyle \mathrm {I} }$-метод Полларда.

Для оптимизированного ${\displaystyle \rho }$-метода Полларда вычислительная сложность оценивается как ${\displaystyle O({\sqrt {q}})}$. Таким образом для обеспечения криптостойкости ${\displaystyle {10}^{30}}$операций необходимо использовать 256-разрядное ${\displaystyle q}$.

Особенностью стандарта ГОСТ Р 34.10-2012 является то, что в документе не зафиксированы какие-либо кривые, рекомендуемые для использования, присутствует только набор требований к ним. Для конкретных примеров кривых, приведенных в стандарте, явно оговорено, что они должны использоваться сугубо в тестовых целях. В этом наш стандарт существенно отличается, например, от документа, определяющего схему ECDSA: в FIPS PUB 186-4 [4] приведены рекомендованные (даже с пометкой "для использования в государственных учреждениях") кривые. С одной стороны, данный подход позволяет сохранять стандарт неизменным даже при появлении новых результатов о "слабых" классах эллиптических кривых: достаточно будет проверить новые ограничения для используемых на практике кривых и при необходимости быстро провести их замену – но не менять государственный стандарт. С другой стороны, отсутствие рекомендуемых для использования параметров требует дополнительных действий от криптографического сообщества по выбору и обоснованию конкретных параметров, а также согласованию их с регулирующими органами и созданию методических рекомендаций.

ФСБ участвует в разработке международного стандарта блокчейна

Свои планы на блокчейн государство обозначило в программе цифровой экономики, которую правительство утвердило в конце июля текущего года. Согласно официального документа в IV квартале 2018 года должны быть готовы проекты нормативных актов, которые бы позволили провести правовой эксперимент по использованию блокчейна для удостоверения прав.